[ad_1]
Previous 7 days I blogged about our Yr 8 assessments. I set out the rules we follow when we produce our Critical Phase 3 assessments, and I shared illustrations of the inquiries that challenged our best attaining pupils.
Present day article is about 12 months 9. My school’s Calendar year 9 cohort has a very vast range of maths attainment, which was further more exacerbated by the lockdowns in 12 months 7 and 8. A single notable element of this 12 months group is how amazingly great the high attaining students are. The top rated set instructor finds it difficult get the job done to adequately problem them in lessons. So when I designed the conclude of 12 months evaluation, I had to make certain there ended up lots of inquiries in there to make them think. I will not want anyone coming out of a maths evaluation bragging that they found it really simple.
In this article are some of the a lot more difficult thoughts from our end of Calendar year 9 assessment.
Ratio
At a live performance the ratio of adult men to women is 5 : 3.
The ratio of ladies to little ones is 7 : 4.
Demonstrate that more than 50 % of the individuals at the live performance are men.
A extra challenging ratio query was this one particular from Edexcel, which also examined an additional Yr 9 matter: shifting the matter.
The ratio (y + x) : (y – x) is equivalent to k : 1.
Find a components for y in phrases of k and x.
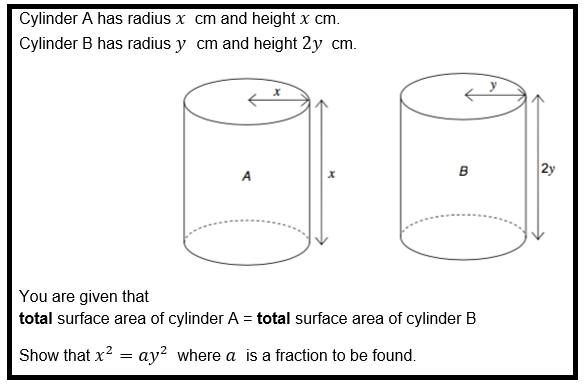
Floor Space
Surface space is a fantastic topic simply because it presents a lot of alternatives for dilemma fixing and reasoning. For case in point, this classic issue could have been quite clear-cut for a large attainer, but I like the way it can be also accessible to any one who does a bit of wondering. I was delighted that a couple students in my class labored this out. We set it in our non-calculator paper so it also examined their arithmetic.
The full area place of a cube is 294cm2.
Work out the volume of the dice.
A a little bit far more tricky problem was this a single from Edexcel. It won’t have any significantly challenging reasoning in it, but has obtained a multiple ways to get the job done through, together with unit conversion which could possibly be skipped. I like thoughts exactly where pupils have to detect that they will need to operate with surface region rather than volume.
The most complicated area location question I included was this 1 from AQA. Extremely handful of college students could do this, even our optimum attainers. We will revisit queries like this in Calendar year 10.
Bounds
I like this coal question from WJEC. In 12 months 9 we instruct bounds and mistake intervals for the very first time. We introduce some fundamental bounds calculations, but go into bigger depth on this at GCSE. This concern fitted properly. Nonetheless, I thought our learners would uncover it less complicated than they did. I had it in the vicinity of the get started of the paper, but most the pupils in my course only picked up just one mark on it. My learners are all doing the job at a Grade 4 level although. Our greater attaining students experienced no problem with this just one.
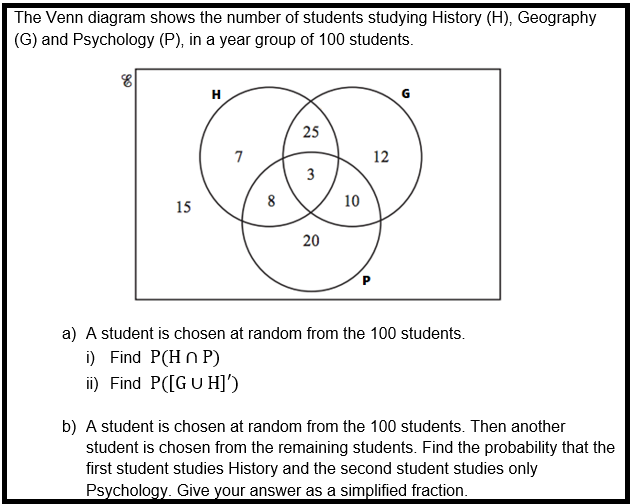
Likelihood
We taught Venn Diagrams to Calendar year 9 this calendar year. There have been some rather simple Venn diagram thoughts nearer the start out of our conclude of year evaluation, in which college students generally just had to entire different Venn Diagrams. But for obstacle I needed to take a look at being familiar with of notation as very well as probability, so I tailored an OCR AS amount dilemma. Only our very greatest mathematicians answered this properly.
Algebraic Proportion
Algebraic proportion can be exceptionally procedural. As very long as learners go through the issue very carefully, the moment they know how to do it, it’s practically a certain five marks. So I incorporated a non-calculator proportion concern that was a little bit distinctive to inquiries they’d noticed prior to. What I appreciated about this was the accessibility: no one from my course acquired all the marks, but they did handle to select up a person or two.
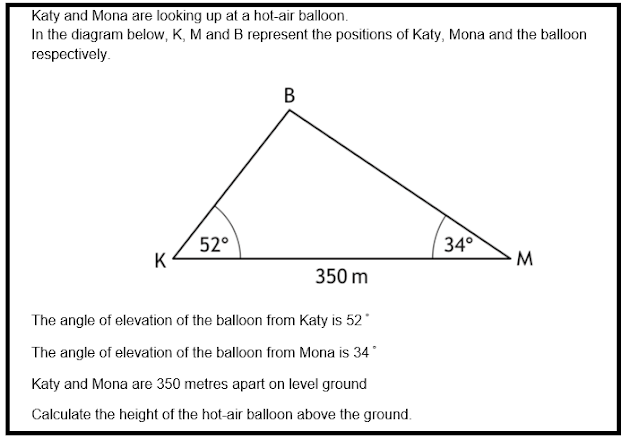
Ideal-Angled Trigonometry
This concern was my pièce de résistance. I figured that if our tremendous clever Yr 9s breezed as a result of all the other hard issues I threw at them, they would certainly have to halt and imagine at this level. This SQA concern is built to be solved applying the Sine Rule. But our college students will not do the Sine Rule right up until 12 months 10. This issue can be completed with ideal-angled trigonometry. The way I did it was by splitting the base into x and 350 – x, then forming two equations for the height and equating them. Even if our students managed to get this much, solving the equation would be fairly tough for them since they have not noticed anything like this prior to.
As it took place, none of our Calendar year 9s managed to clear up it in the way I envisaged. But a single pretty wise college student came up with a genius (albeit inefficient!) method of trial and improvement. I yelped with joy when I realised what he’d performed:
It really is such a delight to see pupils utilizing inventive methods like this.
I also uncovered some terrific complicated queries involving conventional sort and percentages, but I will halt at this place or else this site put up will go on forever! Like I said in my last submit, there are quite a few sites we can uncover good assessment thoughts for Critical Phase 3. It’s a disgrace they are not centrally manufactured any longer – the outdated KS3 SATs contained good thoughts, but at the very least we can still attract on those people to make our possess assessments.
If you have any superior Calendar year 9 evaluation issues you’d like to share, please tweet me.
Thanks for reading!
[ad_2]
Supply link






More Stories
How to Build Connections and Thrive on Campus
Top Campus Life Hacks Every Student Should Know
Campus Myths Debunked: What You Need to Know